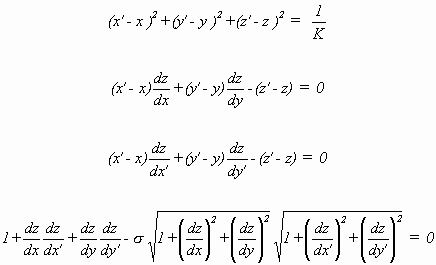
3.4 Die Bäcklundtransformation
ALBERT VICTOR BÄCKLUND gelang es 1883, die von Bianchi gefundene Komplementärtransformation wesentlich zu erweitern [Bäcklund 1883]. Während BIANCHI verlangt hatte, daß die Tangentialebenen entsprechender Punkte senkrecht aufeinander stehen müssen, stellte BÄCKLUND nur die Forderung, daß der Winkel σ zwischen zwei solchen Ebenen konstant sei. In dieser allgemeineren Transformation ist also die Bianchische als spezieller Fall enthalten. Bäcklund griff die von LIE eingeführte Notation der Bianchitransformation auf und verallgemeinerte sie folgendermaßen:
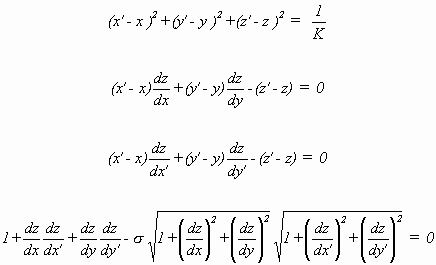
Diese später nach ihm benannte Bäcklundtransformation (genauer: Auto-Bäcklundtransformation der SG-Gleichung) transformiert jede pseudosphärische Fläche bei einmaliger Anwendung in ¥ 1 viele Flächen gleicher Krümmung. Flächen nicht konstanter und negativer Gaußscher Krümmung transformiert sie nicht in Flächen gleicher Art.
BÄCKLUNDS frühe Arbeiten zur von LIE begründeten Theorie der Berührungstransformationen [Bäcklund 1874 - 1883] stehen in enger Verbindung mit den Arbeiten LIEs dieser Zeit, wie in [Kirschnick 1996] gezeigt wird. Man kann den Eindruck bekommen, daß BÄCKLUND Gedanken von LIE erweiterte, neue Details und Verallgemeinerungen hinzufügte. Daher ist einer Äußerung GEORGE L. LAMBs aus einer heute sehr bekannten Arbeit zur Geschichte der Bäcklundtransformation [Lamb 1976, S. 62] zu widersprechen:
"Research on pseudospherical surfaces ... led A. V. Bäcklund to discover, in about 1875, the transformation theory that now bears his name."
LAMB zitierte in diesem Zusammenhang die Arbeit [Bäcklund 1874]. Diese Arbeit und [Bäcklund 1876] sind BÄCKLUNDs ersten zur Theorie der Berührungstransformationen. Sie sind in einem Zusammenhang zu sehen mit Arbeiten LIEs [Lie 1873, 1874], denn in ihnen geht BÄCKLUND auf die Erweiterbarkeit der von LIE untersuchten Berührungstransformationen ein. Der Anstoß zu einer Verallgemeinerung der Lieschen Berührungstransformationen kam erst 1879 durch die Gedanken BIANCHIs zur Transformation pseudosphärischer Flächen aus der Differentialgeometrie. Diese "Befruchtung" der "analytischen Theorie der Punkt- und Berührungstransformationen" durch die Gedanken BIANCHIs markiert den Beginn der Theorie der Bäcklundtransformationen. Die Auto-Bäcklundtransformation der SG-Gleichung schuf LIE daraufhin im gedanklichen Entwurf 1880 (s.o.) und BÄCKLUND explizit erst 1883. Die von LAMB zitierte Arbeit Bäcklunds [Bäcklund 1874] ist eher eine "Vorarbeit" Bäcklunds, die zur Entdeckung der BT hinführte. LAMBs Äußerung zur Entstehung der Theorie der Bäcklundtransformationen wurde vielfach unbesehen dahingehend interpretiert, daß die Bäcklundtransformation 1875 von BÄCKLUND entdeckt wurde [DEGM 1982] [Rogers 1990] [Fordy 1994], eine Jahreszahl die in der Literatur ebenso häufig zu finden ist wie 1883. Eine Bemerkung NOVIKOVs zu diesem Thema ist ebenfalls irreführend [Novikov 1992], der ohne weitere Erklärungen BIANCHI als den Entdecker der Bäcklundtransformation bezeichnete.
GASTON DARBOUX (1842 - 1917) formte die Bäcklundtransformation, die er als verallgemeinerte Bianchitransformation bezeichnete, 1894 in die später üblichen Formen (3.14a,b) um [Darboux 1887, III, §827] und nannte sie "Transformation de Bäcklund". Bilden die Asymptotenlinien die Parameterlinien u = const. bzw. v = const. und der Winkel Φ zwischen den Asymptotenlinien die abhängige Variable, so nimmt die Bäcklundtransformation folgende Gestalt an:
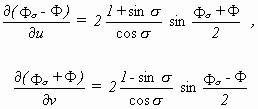
(3.14a)
Diese Transformationsgleichungen implizieren auf die bekannte Weise Integrabilitätsbedingungen. Die Gleichungen kann man so arrangieren, daß eine der beiden Variablen herausfällt, so daß man also wahlweise eine Differentialgleichung für Φ oder eine für Φσ erhält. Es ergibt sich gerade die SG-Gleichung für Φ oder die SG-Gleichung für Φσ. Somit gilt folgendes: Ist Φ = Φ(u,v) eine Lösung der SG-Gleichung, so sind die notwendigen und hinreichenden Bedingungen der Integrabilität von (3.14a) - als Gleichung für Φσ - erfüllt. Die Lösung Φσ = Φσ(u,v) = Φσ(u,v,c) erfüllt die SG-Gleichung und hängt noch von zwei Parametern σ und c ab, wobei c eine Integrationskonstante ist. Die Lösung Φσ = Bσ Φ wird Bäcklundtransformierte von Φ genannt. Sind die Hauptkrümmungslinien die Parameterlinien, so nimmt die Bäcklundtransformation folgende Gestalt an:
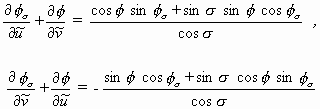
(3.14b)
Kurz nachdem Bäcklund seine Transformationsmethode veröffentlicht hatte, beschrieb 1883 LIE die schon 1880 von ihm geahnte Verknüpfung der Bianchischen mit seiner Transformation zu einer Transformation, die den Zugang zur allgemeinen Lösung der SG-Gleichung schafft. Und es gelang LIE, diese mit der Bäcklundtransformation zu identifizieren [Lie 1883, S. 556]:
"Bezeichne ich Bianchis Operation zur Konstruktion von neuen Flächen konstanter Krümmung mit I, Bäcklunds mit B und meine mit O, so ist es immer möglich, die Konstante in meiner Operation so zu wählen, daß die Relation
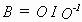
besteht. Bäcklunds äußerst interessante Transformation ist hiermit zurückgeführt auf Bianchis und meine, wobei jedoch zu bemerken ist, daß Bäcklunds Transformation unter den bekannten Voraussetzungen nur Quadratur verlangt, während meine Transformation die Integration einer Riccatischen Gleichung erster Ordnung verlangt."
DARBOUX beschrieb 1894 die Verbindung zwischen Bianchi- und Lietransformation und der Bäcklundtransformation folgendermaßen [Darboux 1887, III, § 811]: Die Bianchitransformation nicht nur auf eine Fläche S angewandt, sondern auf alle durch die Lietransformation transformierten Flächen LσS, entspricht einer Bäcklundtransformation Bσ. Da L0 = 1, geht auch auf diese Weise die Bäcklundtransformation B0 mit σ = 0 in die Bianchitransformation über. Kann man eine pseudosphärische Fläche nebst der Gruppe der aus ihr durch Lies Transformation entstehenden bestimmen, so beruht die weitere Anwendung der Bäcklundtransformation bzw. der Bianchi- und Lietransformation auf die entstandenen Flächen nur auf Differentiation und Elimination. DARBOUX drückte diesen Vorgang in der auch heute üblichen symbolischen Schreibweise folgendermaßen aus:
A. VOSS [Voss 1903] und ihm folgend später andere Autoren [Seeger 1980a] bezeichneten dies als Darbouxschen Satz. Sie übersahen, daß er schon von LIE stammt!
Eine wichtige Vervollkommnung erfuhr die Transformationstheorie für pseudosphärische Flächen 1892 durch einen Satz von BIANCHI, den er als Vertauschbarkeitssatz bezeichnete [Bianchi 1892]. Symbolisch lautet er:
BIANCHI hierzu [Bianchi 1910, §260]:
"Sind zwei pseudosphärische Flächen S1, S2 mit ein und derselben pseudosphärischen Fläche S durch zwei Bäcklundsche Transformationen Bσ1 bzw. Bσ2 mit verschiedenen Konstanten σ1, σ2 verknüpft, so gibt es eine vierte pseudosphärische Fläche S1,2, die nun wieder mit den selben beiden Flächen S1, S2 durch Bäcklundsche Transformationen Bσ1 bzw. Bσ2 mit vertauschten Konstanten verknüpft ist. Offenbar gelangt man von S zu S1,2 entweder, indem man zuerst Bσ1 dann Bσ2, oder indem man zuerst Bσ2 und dann Bσ1 ausführt."
Der speziellere Fall des Vertauschbarkeitssatzes
war von BIANCHI schon 1886 gefunden worden [Bianchi 1886]. Der Vertauschbarkeitssatz hat nun eine wichtige Konsequenz, die zum Ausbau der Transformationsmethode beitrug. BIANCHI zeigte nämlich im Beweis seines Satzes, daß wenn Φ1 und Φ2 die Bäcklundtransformierten einer beliebigen Lösung Φ zu den Konstanten σ1, σ2 sind, (σ1 ¹ σ2) aus dem Vertauschbarkeitssatz folgt:
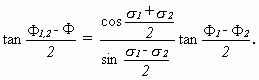(3.15)
Diese Relation ist sehr bemerkenswert, da sie drei Lösungen Φ, Φ1, Φ2 auf rein funktionale Weise (d.h. ohne weitere Integration) eine vierte Lösung zuordnet. Eine solche Relation bezeichnet man heute als nichtlineare Superposition. Eine solche war vordem schon für Lösungen der Riccatigleichung bekannt. Die obige Superposition kann beliebig oft wiederholt werden, so daß eine beliebige Anzahl Bäcklundtransformierter aus einer Anfangslösung Φ generiert werden kann. Insbesondere für die zweimalige Anwendung der gleichen Bäcklundtransformation auf die beliebige Anfangslösung erhält man [Bianchi 1910, § 262]:
wobei c1 eine willkürliche Konstante ist und c = f(σ) eine beliebige Funktion mit f(σ1) = c1. Im Jahre 1899 [Bianchi 1899] entdeckte BIANCHI, daß zwei Bäcklundtransformationen mit komplexen σi auf eine reelle Lösung Φ1.2 führen können, falls Φ1* = Φ2 und σ1* = σ2, bzw. σ1 = σ´+ iσ" und σ2 = σ´- iσ". Die den Lösungen Φ1 und Φ2 entsprechenden pseudosphärischen Flächen sind dann zwar imaginär, die aus der Bäcklundtransformation Bσ1 Bσ2 entstehende Lösung Φ1,2 jedoch ist reell, ebenso wie die ihr entsprechende pseudosphärische Fläche S1,2.
Die Bäcklundtransformation ist - historisch gesehen - als Ergebnis der Synthese zweier Strömungen entstanden: einer geometrischen und einer analytischen. Es gibt somit auch zwei unterschiedliche Betrachtungsweisen, mit denen die Bäcklundtransformation angeschaut werden kann. Die geometrische Betrachtungsweise der Bäcklundtransformation als Flächentransformation in der Art, wie BIANCHI bzw. RIBAUCOUR sie formuliert haben (s.o.), ist mit den Solitonen schwer in Verbindung zu bringen. Zum Verständnis des Solitons trägt vielmehr die analytische Betrachtung der Bäcklundtransformation bei, weil sie zu der Frage führt, wie Linearität und Nichtlinearität miteinander in Beziehung stehen. Eine Solitonengleichung zeichnet sich dadurch aus, daß sie nichtlinear ist und auf die eine oder andere Weise auf lineare Gleichungen rückführbar ist. Diese Eigenschaft ist an der Bäcklundtransformation der SG-Gleichung studierbar. Aus ihr läßt sich durch geschickten Ansatz ein System simultaner Riccatigleichungen ableiten, das sich durch einen wohlbekannten Quotientenansatz linearisieren läßt. So hat man ein lineares System, dessen Integrabilitätsbedingung eben die SG-Gleichung ist, und man hat in dem linearen System noch einen freien Parameter.
Weiter mit Kapitel 3.5: Zur weiteren Entwicklung der Theorie der Bäcklundschen Transformationen