2.3 Mathematische Beschreibungen der solitären Welle
Der erste Mathematiker, der das Problem der solitären Welle mit einem fundierten mathematischen Ansatz anging, war ein Franzose: VALENTIN JOSEPH BOUSSINESQ (1842-1929) . In seinem bedeutendsten Werk zur Hydraulik, dem 700 Seiten starken "Essai sur la théorie des eaux courantes" [Boussinesq 1877], behandelte er systematisch fließende Gewässer in Kanälen und Röhren. Hier finden sich auch frühere Veröffentlichungen von BOUSSINESQ zur solitären Welle zusammengefaßt. Diese früheren Arbeiten zur solitären Wasserwelle sind von BOUSSINESQ sehr schnell hintereinander veröffentlicht worden und bauen z.T. aufeinander auf [Boussinesq 1871a, b, 1872, 1873]. Das Ziel dieser Arbeiten machte er mit dem ersten Satz der ersten Arbeit deutlich [Boussinesq 1871a, S. 755] (Übersetzung des Autors):
"Ich nehme mir vor, theoretisch die Gesetze der von J. Scott Russell und M. Bazin beobachteten Wellen in Kanälen zu begründen ..."
BOUSSINESQs Abhandlungen beantworteten viele damalige Fragen zur Existenz und zu den Eigenschaften der solitären Wasserwelle. Es gelang ihm, die Gesetze der solitären Welle in Gleichungen zu fassen; nämlich in eine partielle Differentialgleichung, die heute nach ihm benannte Boussinesq-Gleichung, in einen Ausdruck für die Form der Welle, eine Lösung der Boussinesq-Gleichung und in einen Ausdruck für die lange diskutierte Geschwindigkeit der solitären Welle, welcher RUSSELLs Versuchsergebnisse exakt bestätigte. Auch weitere Eigenschaften der solitären Welle beschrieb BOUSSINESQ in einer eingehenden Untersuchung der Boussinesq-Gleichung. Der Erfolg seiner Rechnungen liegt im Ansatz begründet. Er verband die bekannten hydrodynamischen Gesetze mit den experimentell gefundenen Eigenschaften der solitären Welle.
BOUSSINESQ untersuchte in seinen vier oben erwähnten Arbeiten Wellen mit der besonderen, von RUSSELL und BAZIN erwähnten Eigenschaft: Sie sollten eine nicht zu vernachlässigende vertikale Bewegung auf die Wassermoleküle übertragen und ferner eine horizontale Bewegung, die nur in erster Näherung unabhängig von z ist. Diese Forderungen gehen über die von LAGRANGE gestellten Bedingungen an sehr lange Wellen hinaus, der die vertikale Bewegung vernachlässigt hatte. Und sie lassen eine z-Abhängigkeit der horizontalen Bewegung zu, wovon EARNSHAW und STOKES abgesehen hatten. BOUSSINESQs Forderungen lassen umfangreichere Beschreibungen zu als nur die der formstabilen, solitären Wellen. Während BOUSSINESQ in seiner ersten Arbeit zu diesem Thema [Boussinesq 1871a] sich nur auf die formstabilen Wellen dieses Typs beschränkte, verallgemeinerte er in seiner zweiten Arbeit [Boussinesq 1871b] den Ansatz, der nun mehr als nur die solitäre Welle einschloß. Die dritte Arbeit [Boussinesq 1872] wiederholt die zweite in einer ausführlicheren Form und schließt weiterführende Betrachtungen an. Die vierte Arbeit schließlich [Boussinesq 1873] ist ein kurzer Anhang zur dritten.
Die Grundzüge von BOUSSINESQs Weg zur heute nach ihm benannten Gleichung seien hier kurz skizziert, da sie bei den später folgenden Betrachtungen der Abhandlungen von RAYLEIGH und von KORTEWEG und DE VRIES als Grundlage dienen sollen. In seinem allgemeinen Ansatz stellte BOUSSINESQ die Forderung nach Formkonstanz - mithin also auch der Konstanz der Geschwindigkeit - der Welle nicht! Es sollte nur u(x,z) wenig von z abhängig sein, d.h. λ > H, ferner H > h und ux klein gegen u.
Aus u = φx und w = φz und der Laplace-Gleichung wz = -ux folgt
![]() (2.11)
(2.11)
Wegen der Bedingung w = 0 für z = 0 kann f(x) = 0 gesetzt werden. Wegen φxz = φzx bzw. uz = vx ergibt sich
![]() (2.12)
(2.12)
Als erste Näherung kann von u = u0(x) ausgegangen werden. u = u0(x) eingesetzt in Gleichung (2.11) liefert ein erstes Ergebnis für w(x,z), welches in Gleichung (2.12) eingesetzt liefert:
![]()
Durch Einsetzen dieses Resultats in Gleichung (2.11) und dies wieder in Gleichung (2.12) usw. ergibt sich für u eine Reihenenwicklung. Für φ folgt daraus
![]() (2.13)
(2.13)
Für die Geschwindigkeiten u1 und w1 eines Teilchens an der Wasseroberfläche folgt aus der Bernoulli-Gleichung (2.4) die Gleichung
![]()
Als Bedingung für die freie Oberfläche erhielt BOUSSINESQ die Relation
![]() (2.14)
(2.14)
Sie ist heute als Kinematic Free Surface Boundary Condition (KFBSC) bekannt [Dea., Dal. 1984]. Einsetzen von Gleichung (2.13) in die Bernoulli-Gleichung für die Wasseroberfläche und in (2.14) liefert
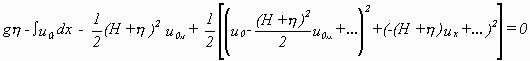
(2.15a)
und
![]() (2.15b)
(2.15b)
Aus diesen Gleichungen folgt in erster Näherung
![]()
und daraus
![]() (2.16)
(2.16)
Die erste Gleichung von (2.16) ist wieder die bekannte d´Alembertsche Gleichung. In einer zweiten Näherung werden die jeweils nächsthöheren Terme aus den Gleichungen (2.15 a, b) mit berücksichtigt:
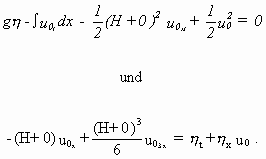
Die kleinen Terme werden durch die Ergebnisse von (2.16) genähert. Aus den dabei entstehenden Gleichungen folgt nun die Boussinesq-Gleichung:
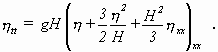 (2.17)
(2.17)
Diese Gleichung machte BOUSSINESQ im folgenden zum Ausgangspunkt seiner ausführlichen Untersuchungen. Von ihr gelangte er mit den gleichen Näherungen (2.16), die ihn zur Boussinesq-Gleichung geführt hatten, zu der Geschwindigkeit der Welle
![]() (2.18)
(2.18)
c ist hier keine Konstante, sondern erlaubt - wie auch die Boussinesq-Gleichung selber - eine Formveränderung der Welle mit der Zeit. Implizit steckt in dem Schritt von (2.17) nach (2.18) auch die Korteweg-de Vries-Gleichung (KdV-Gleichung) selber, denn mit der Näherung (2.16)
![]()
folgt aus Gleichung (2.18) die KdV-Gleichung, wenn auch nur für Wellen in einer Richtung
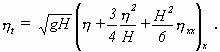
Doch diesen Schritt zu einer neuen Gleichung tat BOUSSINESQ nicht.
Aus der Boussinesq-Gleichung bestimmte BOUSSINESQ die Geschwindigkeiten u(x,z) und w(x,z) eines Wassermoleküls. Ferner bestimmte er die Lage des Massenschwerpunkts der Welle und, daß seine Höhe über dem Niveau des ungestören Wassers sowie dessen Geschwindigkeit konstant ist. Erst nach der Beschreibung dieser Eigenschaften, die allen der Boussinesq-Gleichung gehorchenden Wellen zu eigen sind, wandte sich BOUSSINESQ dem Spezialfall zu, daß die Form der Welle zeitlich konstant sein solle. Diese explizite Forderung erst führte zur konstanten Wellengeschwindigkeit c2 = g(H+h).
Der Vergleich dieser Geschwindigkeit mit Gleichung (2.18) führte BOUSSINESQ zur Gleichung
![]() (2.19)
(2.19)
deren Integration ihn schließlich zu der heute bekannten Ein-Solitonenlösung für die Form der Wasseroberfläche führte (vgl. Abb. 2.8)
![]() (2.20)
(2.20)
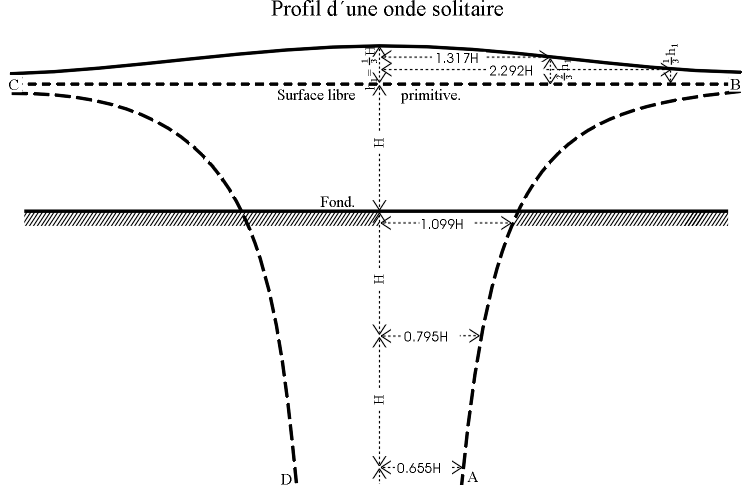
Abbildung 2.8:
BOUSSINESQs Zeichung des Profils der solitären Welle mit der Wellenhöhe h = 1/3 H nach der der Gleichung (2.20) entsprechenden Gleichung
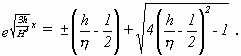
Die beiden heruntergehenden Äste entstehen für h < 0. Aus [Boussinesq 1872].
Zu dieser Lösung war BOUSSINESQ in seiner ersten Arbeit, in der er nur zeitlich konstante Wellen betrachtet hatte, schneller und auch ohne den Umweg über die allgemeinere Boussinesq-Gleichung gekommen. Doch die Boussinesq-Gleichung erlaubte es ihm nun, die zeitlich konstante solitäre Welle als Spezialfall einer allgemeineren Form von Wellen zu betrachten und damit weitgehender zu charakterisieren. So berechnete BOUSSINESQ eine Größe M, die er moment d´instabilité nannte, und die die Schnelligkeit beschreibt, mit der eine Welle ihre Form verändert. Er bewies, daß von allen Wellen gleicher Energie, die der Boussinesq-Gleichung gehorchen, RUSSELLs solitäre Welle die Welle mit der kleinstmöglichem Instabilität M ist. Und daß sie sogar Störungen aus ihrer Form des Gleichgewichts, also Auslenkungen aus der Form (2.20), kompensieren kann, indem sie um diese Gleichgewichtsform oszilliert. Daher - so BOUSSINESQ - sei es so einfach, eine solitäre Welle zu erzeugen, die sich aus einem evtl. sogar turbulenten Anfangszustand von alleine zu einer stabilen Form entwickeln kann. Und ihre Eigenschaften seien daher auch unabhängig von der Art ihrer Erzeugung, eine weitere Einsicht RUSSELLs, die BOUSSINESQ explizit bestätigte.
(Die Arbeit von Miles [Miles 1981] geht besonders auf die Arbeiten von BOUSSINESQ ein, weil sie so oft übersehen wurden. In ihr findet sich auch eine ähnliche Beschreibung der Rechnungen BOUSSINESQs und eine ausführlichere Darstellung von BOUSSINESQs Herleitung des Volumens, der Energie und Stabilität der Welle als Integralinvarianten.)
Mit BOUSSINESQs Arbeiten war nun der Streit um die Existenz und den Charakter der solitären Wasserwelle entschieden, und zwar vollständig zu Gunsten RUSSELLs. BOUSSINESQ hatte RUSSELLs Resultate bestätigt und die solitäre Welle in einigen Punkten noch genauer charakterisieren können. Neben Form, Geschwindigkeit und Stabilität hatte er noch Energie, Volumen und die Schwerpunktslage der Welle berechnen können sowie die Bewegung, die sie auf die einzelnen Wassermoleküle überträgt. Ferner konnte BOUSSINESQ zeigen, daß eine negative solitäre Welle das Bestreben hatte, weitere Wellen an ihrem Ende auszubilden. Daher würde sie - wie RUSSELL schon betont hätte - oszillatorische Wellen hinter sich herziehen. Lediglich auf Kollisionseigenschaften ging BOUSSINESQ nicht ein, da er nur eine einzige Welle betrachtet hatte und niemals mehrere.
In Frankreich wurden BOUSSINESQs Untersuchungen zu Wellen mit großem Interesse aufgenommen. Es ist sein "Essai sur la théorie des eaux courantes" [Boussinesq 1877], der zuerst Beachtung fand und dessen Ergebnisse auch übernommen wurden. So etwa in einem Aufsatz von FLAMANT [Flamant 1889], der es sich zur Aufgabe gemacht hatte, die Kapitel zur solitären Welle aus BOUSSINESQs "Essai" zu einer eigenständigen und einfacher zu verstehenden Arbeit zusammenzufassen. Ebenso ADHÉMAR JEAN-CLAUDE BARRÉ DE SAINT-VENANT (1797 - 1886), der 1885 BOUSSINESQs "Essai" zitierte und versuchte, die Bewegungen der Moleküle an der Wasseroberfläche beim Durchgang einer solitären Welle zu präzisieren [St.-Venant 1885]. Diese Abhandlung hätte eine Abschrift von [Boussinesq 1871a] sein können. Noch zwei Jahre vor BOUSSINESQs recht umfassender Arbeit zur solitären Welle [Boussinesq 1872] hatte SAINT-VENANT eine eigene Behandlung der solitären Welle in Angriff genommen [St.-Venant 1870] und kam auf einer ganz eigenen, eher intuitiven als mathematischen Art auf c2 = g(H+3/2h). Der Unterschied der Ansätze dieser beiden Arbeiten von SAINT-VENANT [St.-Venant 1870, 1885] ist frappierend. Es kann der Eindruck aufkommen, daß SAINT-VENANT von BOUSSINESQs Mathematik so angetan war, daß er sie sich in seiner zweiten Arbeit zu eigen gemacht und ganze Passagen übernommen hatte. Es ist davon auszugehen, daß weder SAINT-VENANT noch FLAMMANT die Arbeit [Boussinesq 1872] kannten (eine an sich eher verwunderliche Tatsache). Sie hätten sich sonst vermutlich nicht die Mühe gemacht, die gleichen Ergebnisse noch einmal aufzuschreiben. Denn weder ist FLAMMANTs Aufsatz kürzer und verständlicher, noch ist ST. VENANTs Arbeit vollständiger als BOUSSINESQs [Boussinesq 1872].
Im übrigen Europa fanden BOUSSINESQs ausgezeichneten Arbeiten über solitäre Wellen wenig Beachtung. Vor allem in Großbritannien, wo besonderes Interesse an der praktischen Nutzung des Wissens über Wellen bestand, hatte die gefühlsmäßige Abneigung der britischen Mathematiker gegen die bei den Franzosen viel stärker ausgeprägte Abstraktion den Austausch mit französischen Naturwissenschaftlern nicht unerheblich behindert [Cros., Smith 1978]. Obwohl BOUSSINESQ seine Arbeiten sowohl in den "Comptes Rendus" wie auch in LIOUVILLEs "Journal de Mathematique" veröffentlicht hatte, den beiden bedeutendsten französischen Zeitschriften für mathematische und angrenzende Gebiete zu jener Zeit, schien man in Großbritannien lange keine Notiz von ihnen genommen zu haben. KORTEWEG und DE VRIES bemerkten in ihrer heute bekannten Arbeit 1895, daß die Motivation zum Schreiben ihrer Arbeit auch von der mangelnden Beachtung der solitären Welle herrührte. Bedeutende britische Autoren wie HORACE LAMB und A. B. BASSET hätten in ihren großen Werken [Lamb 1879], [Basset] zu Wasserwellen nicht klargestellt, daß die solitäre Welle tatsächlich formstabil bleiben kann. Hätte man in Großbritannien BOUSSINESQs Arbeiten mehr Beachtung geschenkt, wäre die Arbeit von KORTEWEG und DE VRIES evtl. nicht entstanden und die Geschichte der Solitonentheorie hätte später einen anderen Verlauf genommen.
Auch JOHN WILLIAM STRUTT (1842-1919), der unter dem Namen Lord RAYLEIGH bekannt ist, waren BOUSSINESQs Arbeiten unbekannt, als er eigene Gedanken zur Russellschen solitären Welle entwickelte [Rayleigh 1876]. Wohl erst nachdem RAYLEIGH seine Abhandlung fertiggestellt hatte, stieß er auf die erste Arbeit BOUSSINESQs zur solitären Welle, wie eine Bemerkung von ihm am Ende seiner Arbeit belegt, nicht jedoch auf die späteren, weiterführenden Arbeiten:
"I have lately seen a memoir by M. Boussinesq ([Boussinesq 1871a]) ..., in which is contained a theory of the solitary wave very similar to that of this paper. So far as our results are in common, the credit of priority belongs of course to M. Boussinesq."
RAYLEIGH entwickelte 1876 fast die gleichen Gedanken wie BOUSSINESQ in seiner ersten Arbeit zur solitären Welle. Sein Ansatz war, eine zeitlich formkonstante Welle in einem fließenden Gewässer zu untersuchen. Ist die Geschwindigkeit des fließenden Wassers so groß wie die Geschwindigkeit der Welle, so wird sie bei entgegengesetzten Geschwindigkeiten eine stehende Welle und die Zeitabhängigkeit entfällt. So gelangte RAYLEIGH auf einem ähnlichen Wege wie BOUSSINESQ zu einer der Gleichung (2.13) entsprechenden Entwicklung. (Ein sehr ausführlicher Überblick mit Kommentaren über die mathematischen Schritte in der Abhandlung von RAYLEIGH [Rayleigh 1876] findet sich in [Bullough 1988]. In [Bull., Cau. 1980] wird in kurzen Stichworten auf die Arbeiten von RAYLEIGH, KORTEWEG und DE VRIES, sowie McCOWAN (s. u.) eingegangen.) Nur hatte RAYLEIGH nicht φ sondern die Stromfunktion ψ in Potenzen von z entwickelt. Abgesehen von diesem Unterschied sind RAYLEIGHs grundlegende Gedanken ähnlich den Boussinesqschen. Und so gelangte er auch mittels der Bernoulli-Gleichung und einigen Näherungen zu
![]()
(vgl. Gleichung (2.19) von BOUSSINESQ) und aus dieser Differentialgleichung zur Lösung
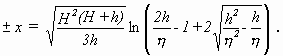
Durch die Näherungen
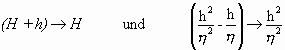
erhält man BOUSSINESQs Ergebnisse (2.19) und (2.20). Ebenso wie BOUSSINESQ gelangte RAYLEIGH zu der Formel für die Geschwindigkeit c2 = g(H+h) der solitären Welle. RAYLEIGH ging auch auf AIRYs und STOKES Kommentare ein, die RUSSELLs Ergebnisse in Frage gestellt hatten. Unter Hinweis auf seine eigenen Ergebnisse konnte er nun RUSSELLs Ergebnisse auch im britischen Raum bestätigen.
Mit RAYLEIGHs Abhandlung fand die Diskussion um die Existenz der solitären Welle nun auch in Großbritannien einen Abschluß. RAYLEIGH war einer der bedeutendsten Naturwissenschaftler und Mathematiker jener Zeit in England, der auch im übrigen Großbritannien und Irland Anerkennung gefunden hatte, und seine Arbeit wurde beachtet. Auch sein Hinweis auf [Boussinesq 1871a] wurde weitergegeben. Es scheint jedoch, als ob RAYLEIGH einer der Wenigen jener Zeit gewesen sei, der einen Blick auf die mathematische Literatur jenseits des Kanals warf, denn außer seinem Hinweis wurde BOUSSINESQ in späteren Arbeiten anderer Autoren zur solitären Welle nicht wieder zitiert. Daher blieben der britischen Wissenschaft die von BOUSSINESQ erst ab 1872 erklärten Eigenschaften der solitären Welle verborgen, die damit ein in Großbritannien noch immer eigentlich unerklärtes Phänomen darstellte. Diesen Zustand beschrieb 1891 McCOWAN [McCowan 1891a, S. 47]:
"... In 1876 Lord Rayleigh ([Rayleigh 1876]) gave another method of approximation leading to an equation for the surface similar to that of Boussinesq ([Boussinesq 1871a]) and the same velocity of propagation. These theories, however, give little further information regarding the wave, and I am not aware that anything further has been done. ... Though the possibility of the propagation of a solitary wave without alteration in form and with constant velocity along a straight canal of rectangular cross-section has not been established on theoretical grounds, yet a result of experiment is such to show that a method based on this assumption must lead at least to a highly approximate account of the motion."
McCowans Kritik an den Ausführungen von BOUSSINESQ und RAYLEIGH fußten auf seiner Annahme, daß die ausgeführten Näherungen nur grob den Eigenschaften der solitären Welle entsprachen, es also nur näherungsweise und nicht streng gezeigt war, daß die solitäre Welle als solche existieren konnte. McCowan versuchte der solitären Welle mit einem allgemeineren Ansatz als RAYLEIGH auf die Spur zu kommen, mit dem Ziel, präzisere Näherungen für Geschwindigkeit und Form der Welle zu bekommen und weitere Eigenschaften beschreiben zu können. Nachdem er wie STOKES zu einer allgemeineren Form der Geschwindigkeit der Welle (Gleichung (2.10)) gelangt war, kam er weiterführend je nach Näherung zu BOUSSINESQs und RAYLEIGHs Ergebnissen oder zu davon leicht abweichenden. Seine abschließende Erklärung, daß STOKES nicht zu den gleichen weiterführenden Lösungen gelangen konnte, weil seine Argumentation bei der Lösung der Laplace-Gleichung einen Fehler enthielte (s.o.), brachte ihm postwendend einen sehr scharfen Gegenkommentar von STOKES ein [Stokes 1891]. Diesen wiederum beantwortete McCOWAN prompt mit einer Richtigstellung [McCowan 1891b]. In späteren Arbeiten u.a. zu solitären Wellen korrigierte McCOWAN eine Bemerkung AIRYs über die Gezeitenwelle [McCowan 1892] und ging auf die Form der Wellen kurz von dem Brechen ein [McCowan 1894].
Ein Jahr später erschien die heute berühmte Abhandlung von DIETERIK JOHANNES KORTEWEG (1848-1941), einem Mathematikprofessor aus Amsterdam, und seinem ehemaligen Doktoranden GUSTAV DE VRIES über lange Wellen in Kanälen, die die Fragen zur solitären Welle beantworten sollte [KdV 1895]. KORTEWEG hatte sich schon in seiner Doktorarbeit, als J. D. VAN DER WAALS erster Student, mit der Wellengeschwindigkeit in Flüssigkeiten beschäftigt [Korteweg 1878]. Im Jahre 1848 hatte HELMHOLTZ gezeigt, daß die Schallgeschwindigkeit in einer kompressiblen Flüssigkeit in einem Rohr von der Elastizität der Rohrwände abhing. In seiner Doktorarbeit lieferte KORTEWEG die dazugehörige Gleichung [Rouse, Ince 1957]. Sein Doktorand DE VRIES wiederum hatte das Thema der solitären Wellen in seiner Doktorarbeit behandelt [Vries 1894], die er am 1. Dezember 1894 an der Universität Amsterdam verteidigte [Kox 1995]. Auch in dieser Doktorarbeit findet sich die heute so gern und oft zitierte und von [SCM 1973] "wiederentdeckte" Geschichte von RUSSELL auf dem Pferd (siehe Fußnote 2, Kapitel 1), ferner eine Beschreibung von RUSSELLs Experimenten in seinem künstlichen Becken und dann eine Theorie der langen, unveränderlichen Wasserwellen, in der auch die KdV-Gleichung zu finden ist [Blij 1978]. Da DE VRIES Doktorarbeit in holländisch verfaßt war, wurde sie ins Englische übersetzt und mit KORTEWEG als Mitautor veröffentlicht [KdV 1895]. So erfuhr sie die Vorstellung in einer breiteren Öffentlichkeit. KORTEWEG und DE VRIES motivierten ihre Abhandlung mit der immer noch fortbestehenden Unsicherheit über die Existenz der formkonstanten solitären Welle [KdV 1895, S. 422]:
"In such excellent treatises on hydrodynamics as those of Lamb and Basset, we find that even when friction is neglected long waves in a rectangular canal must necessarily change their form as they advance, becoming steeper in front and less steep behind."
BASSET hatte die Theorie der solitären Welle knapp behandelt, war jedoch nicht explizit auf den scheinbaren Widerspruch zwischen der Airyschen Theorie langer Flachwasserwellen und der solitären Welle eingegangen [Miles 1981]. Da jedoch weder RAYLEIGH noch McCOWAN [McCowan 1891a] diesen Widerspruch gelöst hätten, wie KORTEWEG und DE VRIES bemerkten, sondern geneigt seien, die solitäre Welle nur als Näherung zu betrachten, sahen sie es als ihr Ziel, diese Frage endgültig zu klären. Aus diesem Beginn der Abhandlung von KORTEWEG und DE VRIES wird klar, daß beide Autoren die weiterführenden Arbeiten von BOUSSINESQ zur solitären Welle [Boussinesq 1871b, 1872, 1873, 1877] nicht gekannt hatten, als sie ihre Abhandlung schrieben. Denn BOUSSINESQ hatte die Frage bereits geklärt. Mehr noch: Die ersten zwei Kapitel ihrer so bekannt gewordenen Abhandlung hätten KORTEWEG und DE VRIES auf wenige Anmerkungen zu BOUSSINESQs Arbeiten reduzieren können, denn ihre Herleitung der von ihnen in dieser Form angegebenen KdV-Gleichung
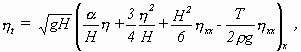
mit α = Konstante und T = Oberflächenspannung, ist im wesentlichen gleich der Herleitung der Boussinesq-Gleichung in [Boussinesq 1872] zusammen mit dem oben erwähnten weiterführenden Schritt zur KdV-Gleichung.
Die Frage liegt nahe, ob KORTEWEG und DE VRIES das Problem der solitären Wellen so gründlich untersucht hätten, wenn die Arbeiten von BOUSSINESQ allgemein bekannt gewesen wären. Denn dann hätten wohl nach 1873 nur noch wenige Fragen zu diesem Thema bestanden. Nun ist, - wie BULLOUGH bemerkte [Bullough 1988] - das Spektralproblem zur Lösung der Boussinesq-Gleichung ein Problem dritter Ordnung (oder eine 3x3 Matrix) und daher ist die Boussinesq-Gleichung mittels der inversen Streutheorie viel komplizierter zu lösen als die KdV-Gleichung, für die das Spektralproblem der Schrödinger-Gleichung genügt. Der bekannte Durchbruch der Solitonentheorie durch die Lösung der KdV-Gleichung mittels der inversen Streutheorie hätte wohl alleine mit der Boussinesq-Gleichung nicht so stattfinden können. Und damit hätte der Beginn der klassischen Geschichte der Solitonentheorie auf eine andere Weise stattfinden müssen als es ab etwa 1967 der Fall war. Die Geschichte der Solitonentheorie wäre anders verlaufen und dieses Gebiet hätte vielleicht heute eine andere Gestalt.
Die Arbeit von KORTEWEG und DE VRIES führt in einigen Punkten weiter als BOUSSINESQs. Eine bedeutende Erweiterung ist die Einführung einer neuen Lösung der KdV-Gleichung, auf die KORTEWEG und DE VRIES durch das Weglassen der Randbedingung η = 0 für ½ x½ ® ¥ stießen:
![]() (2.21)
(2.21)
Hier bezeichnet cn das Jacobische elliptische Integral mit dem Modul M und σ ist eine Integrationskonstante. Die Funktion cn geht für M = 0 in die Sinusfunktion über und für M ® 1 in die solitäre Welle der sech2-Form. Die Boussinesqsche Lösung (2.20) ist also ein Spezialfall der Lösung (2.21). Auf die Existenz solcher Lösungen hatte auch schon BOUSSINESQ hingewiesen [Boussinesq 1877], allerdings ohne sie explizit anzugeben [Miles 1981]. KORTEWEG und DE VRIES schlugen für diese Wellen die originelle Bezeichnung "cnoidale Wellen" vor, in Anlehnung an die Bezeichnung "sinusoidale Wellen". Für die Konstante σ gaben KORTEWEG und DE VRIES an:
![]()
wobei mit T die Oberflächenspannung des Wassers bezeichnet ist. Das Vorzeichen von σ entspricht positiven bzw. negativen solitären Wellen. Für den Fall, daß σ < 0 (und M ® 1), was für Wasser von 20° C ab einer Wassertiefe H unter 4,7 mm der Fall ist, wie KORTEWEG und DE VRIES zeigten, geht die Lösung (2.21) über in
![]()
und diese negative solitäre Welle bleibt stabil. Somit war gezeigt, daß die negative solitäre Welle durch die Einführung der Oberflächenspannung stabil bleiben kann. Während BOUSSINESQ solitäre Wellen gleicher Energie und verschiedener Formen verglich und zu dem Ergebnis kam, daß die solitäre Welle der Form (2.20) die stabilste sei, verglichen KORTEWEG und DE VRIES solitäre Wellen verschiedener Energien und kamen zu dem Schluß, daß die Welle
![]()
nur für den Fall h = h1 unverändert ist. Bei h > h1 werde die Welle vorne steiler und hinten flacher, bei h < h1 vorne flacher und hinten steiler.
Es war KORTEWEGs und DE VRIES Absicht gewesen, mit ihrer Arbeit klarzustellen, daß die von BOUSSINESQ, RAYLEIGH und McCOWAN angegebene Form für die solitäre Welle keine Näherung darstellen muß, sondern eine exakte Lösung für dieses Problem sein kann und daß eine solitäre Welle nicht nur näherungsweise, sondern exakt formkonstant bleiben konnte. Dies galt allerdings nur für eine im Verhältnis zur Wassertiefe bestimmten Wellenhöhe h1. Diese beabsichtigte Klärung scheint ihnen gelungen zu sein. In späteren Abhandlungen zu Wasserwellen wird die Möglichkeit der Existenz der solitären Welle wohl hin und wieder verschwiegen (s.u.) aber nicht mehr geleugnet. Was die nun gut 50 Jahre währende Diskussion um die solitäre Welle allerdings angeht, hätte die Arbeit von KORTEWEG und DE VRIES - neben der Erklärung der negativen Welle und der einzig möglichen Amplitude h1 einer stabilen Welle - auch für Verwirrung sorgen können. Denn die in der Diskussion so wichtige Geschwindigkeit für die solitäre Welle gaben sie an mit
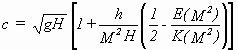
(mit E, K: vollständige elliptische Integrale zweiter und erster Ordnung), was auch im Falle der solitären Welle
![]()
nicht mit der bekannten und mittlerweise oft bestätigten Geschwindigkeit c2 = g(H+h) übereinstimmt. KORTEWEG und DE VRIES hatten jedoch implizit die Geschwindigkeit der solitären Welle so definiert, daß der mittlere horizontale Impuls (über eine Wellenlänge) im bewegten Koordinatensystem (t, X = ct - x) verschwinden sollte [Miles 1981]. Auf diesen diskutierbaren Punkt ihrer Arbeit gingen sie nicht weiter ein.
Die Arbeit von KORTEWEG und DE VRIES als die abschließend klärende Arbeit in der Diskussion um die solitäre Welle zu bezeichnen, ist sicherlich nicht ganz gerechtfertigt. Dafür war auch schon vor 1895 zu viel geklärt. Das Problem war in Frankreich, wie es scheint, schon mit den Arbeiten von BOUSSINESQ und sich anschließenden Arbeiten als gelöst betrachtet worden, denn es sind dort zu diesem Thema keine weiteren Diskussionen zu finden. In Großbritannien hatten RAYLEIGH und McCOWAN die Frage schon so weit zu Gunsten RUSSELLs geklärt, daß es höchstens noch der Erklärung von Details bedurfte, um auch dort das Thema abzuschließen. Ihre große Bedeutung hat die Arbeit [KdV 1895] erst in der heutigen Zeit mit ihrer "Wiederentdeckung" durch GARDNER und MORIKAWA [Gar., Mor. 1960] bzw. ZABUSKY und KRUSKAL [Zab., Kru. 1965] erhalten; hauptsächlich durch die entscheidende Rolle der KdV-Gleichung bei der Etablierung der Solitonentheorie. Diese Rolle hat sie direkt nach ihrem Erscheinen noch nicht gespielt. Eine Biographie über KORTEWEG [Beth, Wou. 1946] geht weder auf seine Arbeiten zu Wasserwellen ein, noch erwähnt sie die heute so bekannte Arbeit von 1895! Was von ihr aufgegriffen wurde, waren in erster Linie die cnoidalen Wellen und nicht die KdV-Gleichung, die schon von KORTEWEG und DE VRIES als "very important equation" bezeichnet wurde. In den Standardwerken zur Hydraulik [Lamb 1932], [Stoker 1957] und [Weh., Lai 1960] fand die KdV-Gleichung keine Erwähnung, jedoch wurden die cnoidalen Wellen z.T. ausführlich behandelt [Miles 1981]. Durch die große Bedeutung, die die KdV-Gleichung heute durch die Solitonentheorie erhalten hat, ist sie auch in das Zentrum der historischen Betrachtungen zur Solitonentheorie gelangt. Kaum eine historische Abhandlung oder Einleitung eines Lehrbuches geht nicht auf die Entdeckung der KdV-Gleichung 1895 ein. Anders steht es mit den Arbeiten BOUSSINESQs zu Wellen. Während ihnen in der Geschichte der Solitonentheorie des letzten Jahrhunderts große objektive Bedeutung zukommt, sind sie in der Sekundärliteratur zur Geschichte der Solitonentheorie bisher kaum besprochen. Lediglich [Miles 1981] geht ausführlicher auf die Arbeiten BOUSSINESQs zur solitären Welle ein. Interessanterweise wird, wenn BOUSSINESQ heute erwähnt wird, meist immer noch seine im Vergleich zu späteren Arbeiten recht unbedeutende Arbeit [Boussinesq 1871a] zitiert, in der die Boussinesq-Gleichung nicht vorkommt. Hier scheint RAYLEIGHs vielzitierte Abhandlung [Rayleigh 1876] bis in die heutige Zeit zu wirken, denn er war es, der nur [Boussinesq 1871a] gekannt, zitiert und damit bekannt gemacht hatte.
Während die KdV-Gleichung selbst in den Jahrzehnten nach ihrer expliziten Entdeckung durch KORTEWEG und DE VRIES keine Beachtung fand, waren Flachwasserwellen und insbesondere die cnoidalen Wellen mit und ohne Berücksichtigung der Oberflächenspannung auch in den folgenden Jahrzehnten bis in die Gegenwart hinein Gegenstand mancher Untersuchungen. In diesem Zusammenhang wurde die Arbeit [KdV 1895] auch hin und wieder zitiert wie eine Übersicht in [Blij 1978] zeigt: In [Lamb 1906] findet sich ein Hinweis auf die Arbeit, und auch in einem Übersichtsartikel in der Encyclopädie der Mathematischen Wissenschaften [Love 1911] wird auf cnoidale Wellen eingegangen, mit einem Hinweis auf [KdV 1895]. Auf dem ersten Internationalen Kongress für Angewandte Mechanik 1924 in Delft behandelte LEVI-CIVITA permanente Schwerewellen [Levi-C. 1925] und es folgten [Dubreil 1924], [Struik 1926], [Kármán 1940], [Keller 1948] und weitere. Aus mathematischer Sicht war ferner die Frage nach den Existenzbeweisen solitärer Wellen interessant und es wurde bewiesen, daß die Eulergleichungen solitäre Wellenlösungen aller Amplituden zulassen. Bemerkungen zu verschiedenen Existenzbeweisen permanenter Schwerewellen findet sich in dem Übersichtswerk [Zeidler 1971]. Aus der Sicht der Mechanik und Ingenieurwissenschaften stand die praktische Anwendung im Vordergrund. Auf diesem Gebiet lieferte [Stoker 1957] eine detaillierte Übersicht.
Weiter mit Kapitel 3: Geometrische Darstellung und Bäcklundtransformation